Modélisation d'un match de Tennis par Chaînes de Markov
Projet de Data Science et d'Analyse Statistique
Contexte et Problématique
Ce projet explore une question fondamentale du tennis à travers le prisme de la science des données : le système de score amplifie-t-il ou diminue-t-il la différence de compétence entre deux joueurs ? Pour y répondre, j'ai modélisé un match de tennis (jeu, set et match) à l'aide de chaînes de Markov en MATLAB, avant de confronter mon modèle aux statistiques réelles de joueurs professionnels.
Aperçu rapide
- Probabilité de victoire (jeu / set / match) en fonction de p
- dP/dp : l’« effet amplificateur » du système de score
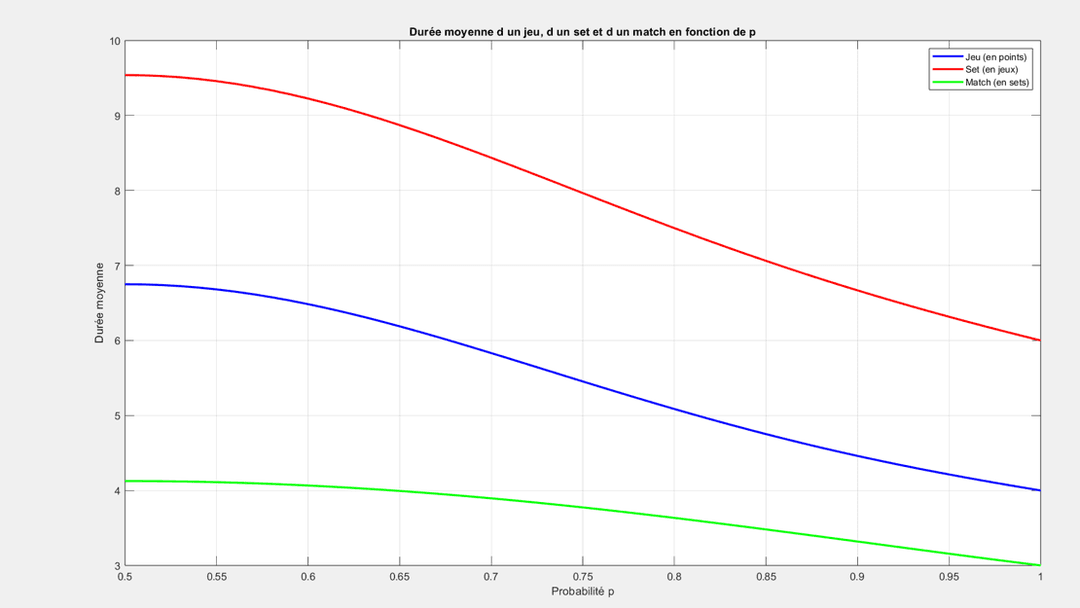
- Durée moyenne (nombre de points, de jeux, de sets)
- Validation empirique sur +13 000 points ATP (Nadal, Simon, Moutet)
Partie 1 : La Modélisation - Traduire le Tennis en Mathématiques
La première étape, et la plus fondamentale, était de construire un modèle mathématique fiable du jeu, du set et du match.
1.1 - Le Jeu : La Brique Élémentaire
Pourquoi une Chaîne de Markov ?
Un jeu de tennis est une séquence de scores où le prochain état ne dépend que du score actuel. Cela correspond parfaitement à un processus de Markov, ce qui m'a permis de modéliser le jeu avec une seule variable : p, la probabilité qu'un joueur gagne un point.
La Construction du Modèle
J'ai défini 18 états de transition (les scores) et 2 états d'absorption (Victoire/Défaite), formalisés dans une matrice de transition de 20x20.
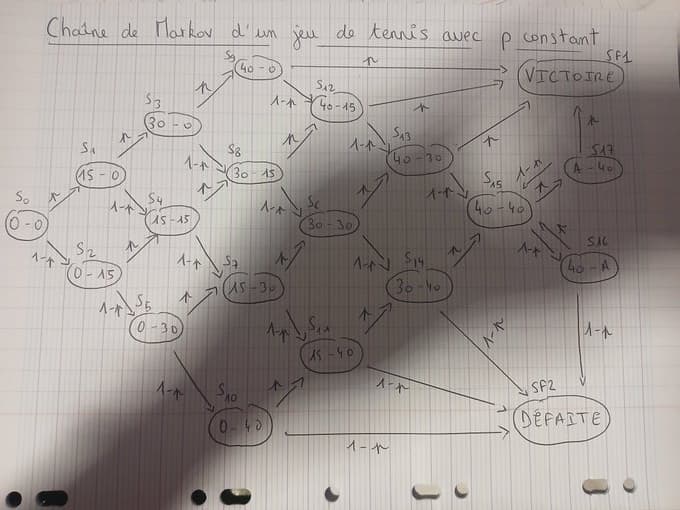
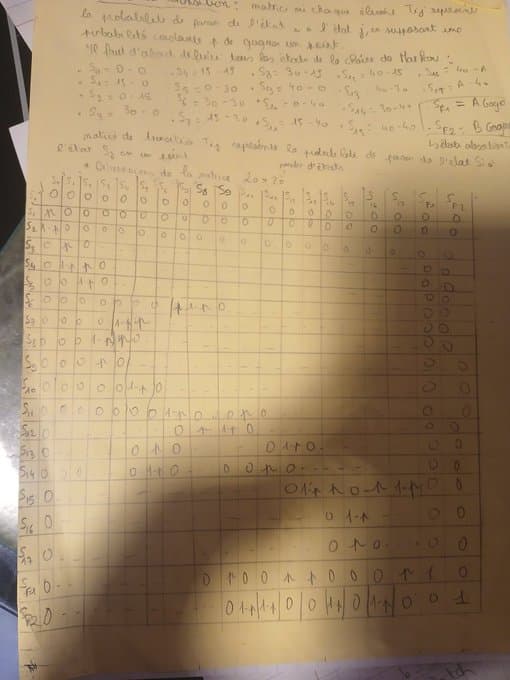
1.2 - Le Set et le Match : La Montée en Échelle
J'ai appliqué la même logique au set (41 états) et au match (11 états). La création manuelle étant impossible, j'ai développé des scripts en MATLAB pour générer ces matrices de transition automatiquement.
Partie 2 : L'Analyse Théorique - Ce que Disent les Modèles
2.1 - Probabilité de Victoire : Une Première Hiérarchie
Pourquoi cette analyse ?
En traçant la probabilité de gagner un jeu, un set et un match en fonction de p, on observe que ces probabilités augmentent naturellement avec la compétence (p). Dans ce modèle, p représente la probabilité de gagner l'unité de base : le point pour le jeu, le jeu pour le set, et le set pour le match. Cependant, plus la courbe est raide autour de p = 0.5, plus le système de score agit comme un amplificateur : une petite différence de niveau entre deux joueurs se traduit par un écart important dans la probabilité de victoire.
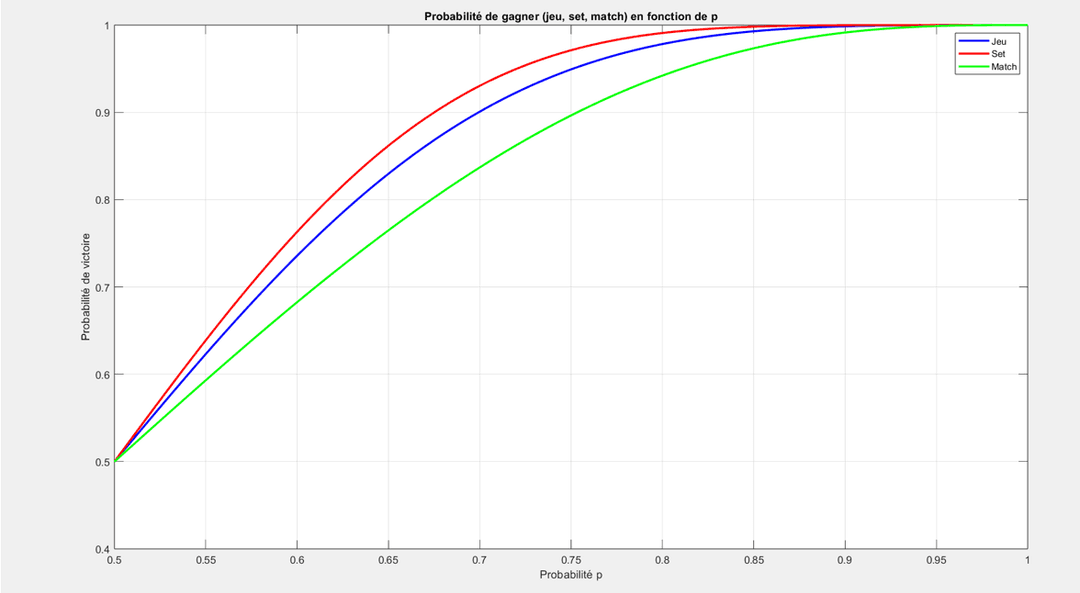
La courbe du set est la plus raide, suivie de celle du jeu, puis du match (dans ce modèle simplifié). Cela suggère que le set est le niveau où les petites différences de compétence ont le plus d'impact.
2.2 - L'Effet Amplificateur : La Dérivée comme Mesure d'Impact
Pourquoi cette analyse ?
Pour quantifier précisément cette "raideur", j'ai calculé la dérivée de chaque courbe. Cette valeur représente l'effet amplificateur : de combien les chances de gagner augmentent pour une petite amélioration de p.
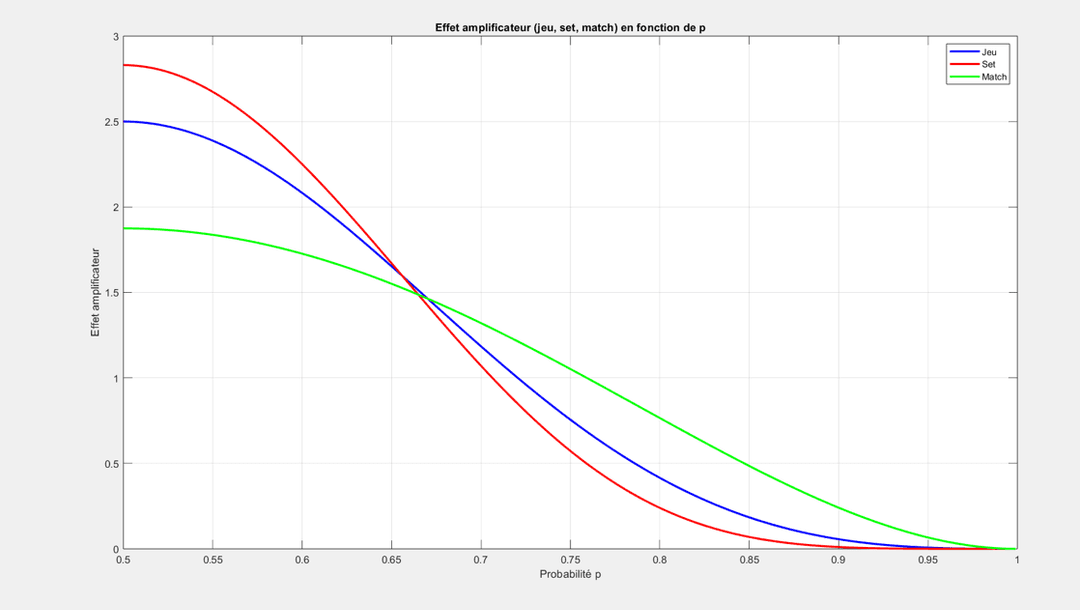
L'effet amplificateur est maximal à p=0.5 pour tous les niveaux. Le set est le plus grand amplificateur pour les joueurs de niveau très proche. Fait intéressant, les courbes se croisent vers p≈0.65, indiquant une dynamique plus complexe pour les joueurs ayant déjà un avantage.
Conclusion : Le set est le plus grand amplificateur pour les joueurs de niveau très proche.
2.3 - Durée de Vie et Situations d'Égalité : Les Mécanismes de l'Amplification
Pourquoi cette analyse ?
L’amplification est d’autant plus marquée que la rencontre est longue : plus il y a de points joués, plus une petite différence de niveau (p) entre les joueurs peut s’accumuler et influer significativement sur l’issue. C’est pourquoi j’ai analysé la durée moyenne d’un jeu, d’un set et d’un match, ainsi que la fréquence des situations d’égalité (comme le score 40–40), où la pression est maximale.
Comment je l'ai fait ?
La durée de vie a été calculée via la matrice fondamentale N = (I - Q)⁻¹. Pour les égalités, j'ai simulé des milliers de parties.
Focus sur le "Deuce" (40-40)
La règle du "deuce" (gagner par deux points d'écart) est un mécanisme d'amplification en soi. Mon analyse a montré que même en partant de 40-40, l'effet amplificateur reste maximal à p=0.5, confirmant son rôle crucial. (Voir l'analyse complète avec rapport + codes sur mon dépôt GitHub)
Focus sur les Scores d'un Set : La Simulation par Heatmap
Pour visualiser concrètement comment un léger avantage se traduit dans un set, j'ai réalisé une simulation de 10 000 sets en considérant un Joueur A avec une probabilité p= 0.55 de gagner chaque jeu. Le résultat est une heatmap (carte de chaleur) qui montre les scores finaux les plus probables.
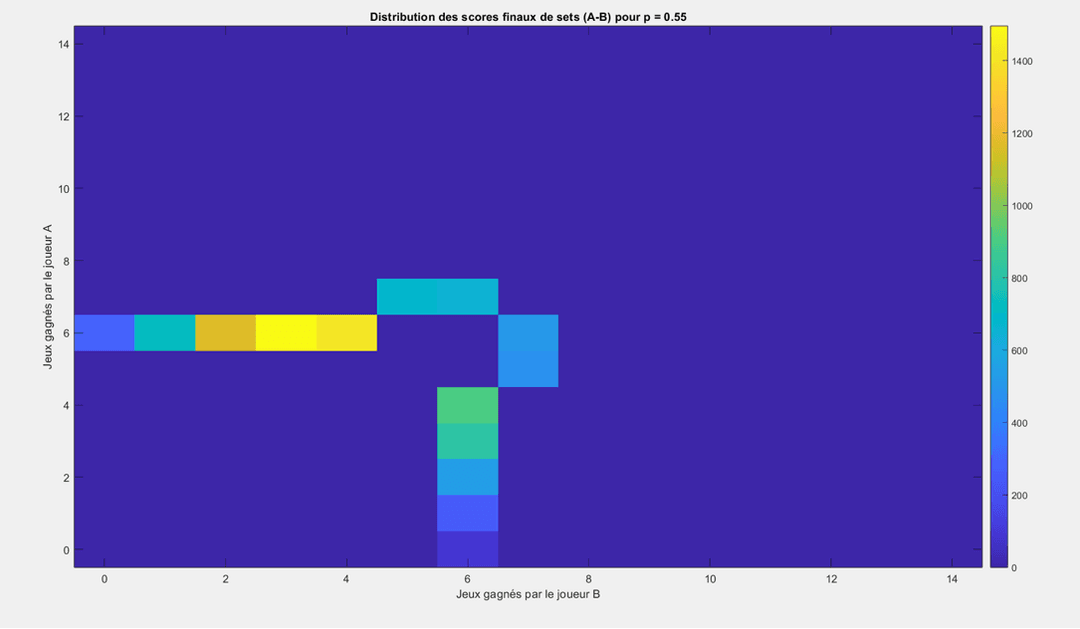
Heatmap pour un Joueur A avec une probabilité de gagner un jeu de p=0.55. On voit clairement que le score le plus fréquent est 6-3. Cela illustre parfaitement comment un avantage de seulement 5% se transforme en une victoire de set avec une marge confortable.
Partie 3 : Le Verdict - Confrontation avec la Réalité
J'ai testé le modèle sur les statistiques de carrière de Rafael Nadal, Gilles Simon et Corentin Moutet, en comparant les prédictions du modèle à leurs résultats réels (données de Tennis Abstract).
Pour chaque joueur, j'ai pris son % de points gagnés comme p et j'ai comparé la prédiction de mon modèle à son % de jeux/sets/matchs gagnés réel.
| Niveau du joueur | Joueur | Prédiction | Réalité | Écart |
|---|---|---|---|---|
| Jeu | ||||
| Exceptionnel | Nadal | 60.9 % | 59.7 % | +1.2 % |
| Bon | Simon | 51.8 % | 51.3 % | +0.5 % |
| Moyen | Moutet | 46.5 % | 47.1 % | −0.6 % |
| Set | ||||
| Exceptionnel | Nadal | 75.6 % | 77.1 % | −1.5 % |
| Bon | Simon | 53.7 % | 53.6 % | +0.1 % |
| Moyen | Moutet | 41.8 % | 43.2 % | −1.4 % |
| Match (Grand Chelem) | ||||
| Exceptionnel | Nadal | 94.7 % | 87.3 % | +7.4 % |
| Bon | Simon | 60.6 % | 59.9 % | +0.7 % |
| Moyen | Moutet | 43.1 % | 47.1 % | −4.0 % |
Les prédictions pour le jeu et le set sont remarquablement précises, validant fortement le modèle. Pour le match, les écarts augmentent, ce qui s'explique par les limites du modèle, notamment l'hypothèse de p constant et le filtrage des statistiques (uniquement les Grands Chelems).
Conclusion Finale et Limites du Modèle
Oui, le système de score au tennis est un puissant amplificateur de compétence lorsque les joueurs sont de niveau proche, mais cet effet s’atténue fortement en cas de grand écart entre eux. Mon analyse, de la modélisation à la validation, le confirme. Chaque palier du système de score (point → jeu → set → match) est conçu pour accentuer les petites différences de niveau.
Limites et Perspectives
Ce modèle est une simplification. Les principales limites sont :
- Probabilité p constante : Ne prend pas en compte la fatigue, la pression ou la surface.
- Absence de distinction service/retour : Le service est un avantage majeur non modélisé ici.
- Hiérarchie non dynamique : Chaque niveau (jeu, set, match) est modélisé indépendamment avec une nouvelle valeur de p, sans héritage des niveaux inférieurs. Cela conduit à une conclusion trompeuse : le match semble amplifier moins que le set, alors qu’en réalité il cumule les effets du set et du jeu. Un modèle hiérarchique complet montrerait qu’il est au contraire l’amplificateur ultime.
Intégrer ces éléments serait une suite logique passionnante pour rendre le modèle encore plus fidèle à la réalité complexe du tennis professionnel.
Le code MATLAB et le rapport d'analyse complet sont disponibles sur GitHub.
Voir le projet sur GitHub